Supereksponento

En matematiko, supereksponento aŭ 4-hiperoperatoro estas ripetita eksponenta funkcio, la sekva hiperoperatoro post potencigo.
Jen estas la unuaj kvar hiperoperatoroj, kaj supereksponento estas la kvara:
- 1 Adicio
- :
- 2 Multipliko
- :
- 3 potencigo
- :
- 4 Supereksponento
- :
kie ĉiu operacio estas difinita kiel ripetado de la antaŭa.
Adicio (a+b) estas b-foja ripeto de la "adicio de 1" aplikata al a, multipliko (ab) estas ĉena adicio de b nombroj a, potencigo ab estas ĉena multipliko de b nombroj a. Analoge, supereksponento ba estas ĉena potencigo de b nombroj a. La parametro a estas la bazo kaj la parametro b estas la alto-parametro.
La unua tri operatoroj - adicio, multipliko kaj potencigo - povas esti ĝeneraligita por kompleksaj valoroj de ambaŭ argumentoj. Sed por supereksponento ĉi tia bona regula ĝeneraligo ne estas ankoraŭ trovita. Iuj provoj de ĝeneraligo estas priskribitaj pli sube, sed ili ne estas sufiĉe bonaj. Tiel supereksponento ne estas konsiderata kiel elementa funkcio.
Gravas ke en kalkulado de multnivela potencigo, la potencigo estas farita ekde la plej profunda nivelo (en la skribmaniero, ekde la plej supra nivelo):
Se fari la potencigon en la mala ordo rezultiĝas ĝenerale la alia valoro, ekzemple:
La alia varianto de supereksponento povas esti enkondukita por la dua varianto, tamen ĉi tiu okazo povas esti skribita kiel
Estas ankaŭ la aliaj similaj al supereksponento esprimoj:
| Supereksponento | a estas la bazo, kaj la kvanto de a estas la alto | |
| Supereksponento de malfinia alto (vidu sube pli detale) | a estas la bazo | |
| Ripetitaj eksponentoj | a estas la bazo, kaj la kvanto de a plus 1 por x estas la alto | |
| Nestitaj eksponentoj | n estas la alto, la bazoj ai povas estas malsamaj. | |
| Malfiniaj nestitaj eksponentoj |
Skribmaniero
La skribmanieroj por supereksponento estas:
| Nomo | Skribo | Priskribo |
|---|---|---|
| Norma skribmaniero | ba | |
| Notacio de Knuth | Permesas vastigaĵo per uzo de pli multaj sagoj, aŭ per indeksita sago. | |
| Ĉena indikila skribmaniero de Conway | Permesas vastigaĵon per uzo de pli granda nombro anstataŭ 2 en la fino (ekvivalento al la vastigaĵo pli supre), kaj ankaŭ per etendo de la la ĉeno. | |
| Akermana funkcio | Taŭgas nur por parta okazo a=2. | |
| Ripetita eksponento | Permesas simplan vastigaĵo al ripetitaj eksponentoj kun komenca valoro ne egala al 1. Ĉi tie kun n fojoj de a. | |
| Hiperoperatoro | Permesas vastigaĵo per uzo de pli granda nombro anstataŭ 4. | |
| Askia skribmaniero de notacio de Knuth | a^^b | La supren-sago estas anstataŭigita per la ĉapelo ^. |
La skribmanieroj por ripetita eksponento estas:
| Nomo | Skribo | Priskribo |
|---|---|---|
| Norma skribmaniero | Ĉi tie kun n fojoj de a. | |
| Notacio de Knuth | Permesas vastigaĵo per uzo de pli multaj sagoj, aŭ per indeksita sago. | |
| Skribmaniero de Ioannita Galidakis | Uzata en [1]. | |
| Askia helpa | a^^n@x | Bazita sur konsidero ke ripetita eksponenta funkcio estas helpa supereksponento. |
| Askia norma | exp_a^n(x) | Bazita sur norma skribmaniero. |
Ekzemploj
La valoroj enhavantaj dekuman komon estas proksimumaj.
| n | 2n | 3n | 4n |
|---|---|---|---|
| 0 | 1 | 0 | 1 |
| 1 | 1 | 1 | 1 |
| 2 | 4 | 16 | 65536 |
| 3 | 27 | 7 625 597 484 987 | |
| 4 | 256 | ||
| 5 | 3125 | ||
| 6 | 46656 | ||
| 7 | 823543 | ||
| 8 | 16 777 216 | ||
| 9 | 387 420 489 | ||
| 10 | 10 000 000 000 |
Vastigaĵoj
Vastigaĵo de bx al reelaj nombroj estas simpla. Por ĉiu natura nombro , estas super-potenca funkcio f(x) = bx.
Vastigaĵo al bazo 0
Iam 00 estas prenita al esti nedifinita valoro. En ĉi tiu okazo, valoro k0 ne povas esti difinita rekte. Tamen, estas bone difinita kaj ekzistas:
Ĉi tiu limigo veras ankaŭ por negativaj n. k0 povita esti difinita per ĉi tiu limigo kaj ĉi tio devus konsenti kun difino de . Ĉi tiu limiga difino tenas por ĉar 2 estas para, kaj tenas por ĉar 0 estas (eĉ, ebena, para).
Vastigaĵo al kompleksaj bazoj
Pro tio ke kompleksaj nombroj povas esti altigita al potencoj, supereksponento povas esti aplikita al bazoj de formo z = a + bi, kie i estas la imaginara unuo.
Ekzemple, en kalkulo de ki per uzo de ĉefa branĉo de la natura logaritmo, kaj de eŭlera formulo rezultiĝas:
Ĉi tio donas rikuran difinon por per :
| Proksimuma valoro | |
|---|---|
| i | |
| 0,2079 | |
| 0,9472 + 0,3208i | |
| 0,0501 + 0,6021i | |
| 0,3872 + 0,0305i | |
| 0,7823 + 0,5446i | |
| 0,1426 + 0,4005i | |
| 0,5198 + 0,1184i | |
| 0,5686 + 0,6051i |
Solvante la inversan rilaton, rezultiĝas kaj , kaj pluaj negativaj valoroj de k donas malfiniajn rezultojn sur la imaginara akso. Grafike prezentita en la kompleksa ebeno, la tuta vico spiralas al la limigo 0,4383 + 0,3606i kiu povis esti interpretita kiel la valoro se k estas malfinio.
Ĉi tiaj supereksponentaj vicoj estis studita ekde la tempo de Eŭlero sed estas malbone) komprenita pro sia kaosa konduto. Plej parto de publikaĵoj fokusiĝis sur la konverĝo de la potenca turo. Aktuala esplori grande plisukcesiĝis per uzo de komputiloj kun fraktala kaj signa matematika programaro. Multo de tio kio estas sciata pri supereksponento venas de ĝenerala scio de kompleksa dinamiko kaj specifa esploro de la eksponenta funkcia mapo.
Vastigaĵo al malfiniaj altoj


Supereksponento povas esti etendita al malfinia alto. Ĉi tio estas ĉar por bazoj en certa intervalo supereksponento konverĝas al finia valoro kiam la alto strebas al malfinio. Ekzemple, konverĝas al 2, kaj povas pro tio estas konsiderata kiel egala al 2. La tendenco al 2 povas vidiĝi per komputado de malgranda finia turo:
Ĝenerale, la malfinia potenca turo , difinita kiel la limigo de kiam n iras al malfinio konverĝas por , proksimume en la intervalo 0,066 ... 1,44. Por ajna reela r kun 0 < r < e, estu , tiam la limigo estas r; ne estas konverĝo por pro tio ke la maksimumo de estas .
Ĉi tio povas esti etendita al kompleksaj nombroj z:
kie estas W funkcio de Lambert. Pro tio ke la limigo devas kontentigi , h(z) estas la suba branĉo de la retroĵeto de .
Vastigaĵo al negativaj altoj
Supereksponento povas esti etendita al negativaj altoj. Pro rilato:
(kiu sekvas de la difino de supereksponento), eblas derivi (aŭ difini) valorojn de kie .
Ĉi tiu konfirmas la intuicia difinon de kiel simple n. Tamen, pluaj valoroj ne povas esti derivitaj per plua ripeto en ĉi tiu maniero ĉar estas nedifinita.
Simile, pro tio ke estas nedifinita:
la derivaĵo pli supre ne validas se n = 1. Pro tio, devas resti nedifinita. Tamen povas sekure esti difinita kiel 1.
Vastigaĵo al reelaj altoj
Je ĉi tiu tempo ne estas kutime akceptita solvaĵo al la ĝenerala problemo de etendanta supereksponento al la reela aŭ kompleksaj valoroj de b, kvankam ĝi estas sub aktiva esploro.
Ĝenerale la problemo estas trovado de supereksponenta funkcio super reela x > -2 tia ke:
- Kvara postulo estas kutime unu el:
- : Kontinueco - ke estas kontinua je ambaŭ variabloj por x > 0
- : Derivebleco - ĝi povas unufoje, dufoje, n-foje, aŭ malfinie diferencialebla je x.
- : Reguleco (enhavanta dufojan diferencialeblecon je x)
- :: por ĉiuj x > 0
La kvara bezono diferencas de aŭtoro al aŭtoro, kaj inter manieroj. Estas du ĉefa manieroj al etendo de supereksponento al reela altoj, unu estas bazita sur la reguleca postulo bezono, kaj unu estas bazita sur la derivebleca postulo. Ĉi tiuj du manieroj aspekti al esti tiel malsama ke ili povas ne esti kunigitaj, ĉar ili produktas rezultojn nekonsekvencajn unu kun la alia.
Solvaĵo kiu kontentigas iun el ĉi tiuj postuloj en intervalo de longo 1 povas esti etendita al solvaĵo por ĉiuj pozitivaj reelaj nombroj. Kiam estas difinita por intervalo de longo unu, la tuta funkcio facile sekvas por ĉiuj x > -2.
La lineara proksimumigo estas:
de ĉi tie:
| por | |
| por | |
| por | |
| ... | |
Ĝi estas kontunua sed nur popeca diferencialebla; je entjeraj valoroj de x la derivaĵo estas multiplikita per ln a.
La kvadrata proksimuma kalkulado estas:
kiu estas diferencialebla por ĉiuj x > 0, sed ne dufoje diferencialebla.
En difino de por ĉiu a, alia ebla bezono povis esti ke ĝi estu monotone pligrandiĝanta kun a.
Vastigaĵo al kompleksaj altoj

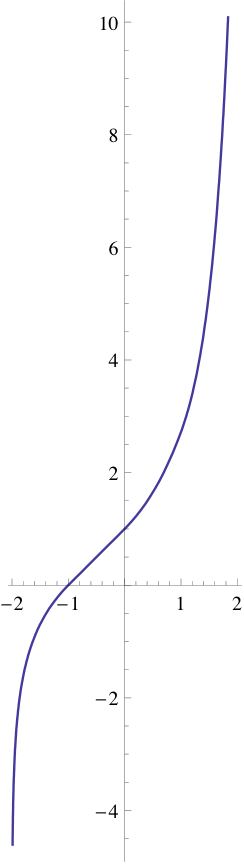
Niveloj kaj
niveloj estas montrita kiel dikaj kurboj.
Ekzisto de analitika vastigaĵo de al kompleksaj valoroj de z estas ankoraŭ ne trovita. Por a=e, ĝi povis esti solvaĵo de la funkcia ekvacio kun aldonaj kondiĉoj ke F(0)=1 kaj F(z) restas finia kiel . Se tia vastigaĵo ekzistas, ĝi povus havi la formon montrita en la bildo dekstre. Ĉi tiu funkcio estas ne tuta, ĉar estas specialaĵoj de F(z) sur la reela akso je la punktoj z = -2, -3, -4, ....
Retroĵetoj
La retroĵetoj de supereksponento estas nomataj kiel superradiko aŭ hiper-4-radiko kaj la superlogaritmo aŭ hiper-4-logaritmo. La kvadrata superradiko ssqrt(x) kiu estas retroĵeto de povas esti prezentita kun la W funkcio de Lambert:
La superlogaritmo estas difinita por ĉiuj pozitivaj kaj negativaj reelaj nombroj b.
La funkcio havas propraĵojn:
La ripetita logaritmo estas iom simila al la superlogaritmo.
Supereksponenta funkcia kreskado
Supereksponenta funkcio kreskas eĉ pli rapide ol duopa eksponenta funkcio .
Ekzemple, por bazo 10 kun la lineara proksimumigo:
- (guglo)
- (gugloplekso)
je .
Vidu ankaŭ
- Notacio de Knuth
- Akermana funkcio, inversa akermana funkcio
- Hiperoperatoro
- Superlogaritmo
- Superradiko
- Ripetita logaritmo
Eksteraj ligiloj
- Tetration de Daniel Geisler
- Potenca turo je MathWorld
- Supereksponenta forumo
- Etendado hyper4 al neentjeroj Ŝablono:Webarchiv (nedatita, 2006 aŭ pli frua). Ioannis N. Galidakis.
- Etendado hyper4 kaj supren-saga skribmaniero de Knuth al reelaj nombroj Ŝablono:Webarchiv (nedatita, 2006 aŭ pli frua). Ioannis N. Galidakis.
- Vastigaĵo de la hiper4 funkcio al reelaj nombroj - neformala diskuto pri etendado de supereksponento al la reelaj nombroj. Robert Munafo.
- Supereksponento de la kvadrata radiko de 2, (2004). Provo etendi supereksponenton al reelaj nombroj. Lode Vandevenne.
- [1] Ŝablono:Webarchiv Definitiva listo de referencoj al supereksponentaj esploroj. Parceloj de informo sur la W funkcio de Lambert, rimanaj surfacoj, kaj analitika vastigado. Ioannis N. Galidakis.
- Iuj kritikaj punktoj de la hiperpotenca funkcio Ŝablono:Webarchiv, Joseph MacDonell.
- TTT-paĝoj por malfinie ripetitaj eksponentoj - kompilaĵo de elementoj de demandoj pri supereksponento, Dave L. Renfro.
- Ŝablono:Citaĵo el la reto Hejmo de supereksponento - malfinie diferencialebla vastigaĵo de supereksponento al reelaj nombroj