Transformo de Möbius

Transformo de Möbius devus esti ne konfuzita kun la konverto de Möbius kaj la funkcio de Möbius.

En matematiko, Transformo de Möbius estas bijekcia konforma bildigo de la etenda kompleksa ebeno (kio estas la kompleksa ebeno pligrandigita per la punkto je malfinio):

$\widehat{ℂ}=ℂ\cup \{\mathrm{\infty }\}.$

La aro de ĉiuj transformoj de Möbius formas grupon sub komponaĵo nomita kiel la grupo de Möbius. Transformoj de Möbius estas nomataj ankaŭ kiel frakciaj linearaj transformoj.

Ĝenerala priskribo

La möbius-a grupo estas la aŭtomorfia grupo de la rimana sfero

$\text{Aut}(\widehat{ℂ}).$

Certaj subgrupoj de la möbius-a grupo formas aŭtomorfiajn grupojn de la aliaj simple-koneksaj rimanaj surfacoj (la kompleksa ebeno kaj la hiperbola ebeno). Kiel tia, möbius-aj transformoj ludas gravan rolon en la teorio de rimanaj surfacoj. La kovranta grupo de ĉiu rimana surfaco estas diskreta subgrupo de la möbius-a grupo (vidu grupon de Klein). möbius-aj transformoj estas ankaŭ proksime rilatanta al (izometrioj, izometrias) de hiperbolaj 3-duktoj.

Aparte grava subgrupo de la möbius-a grupo estas la modula grupo; ĝi estas centralo al la teorio de multaj fraktaloj, modulaj formoj, elipsaj kurboj, kaj Pellia ekvacioj.

En fiziko, la identa komponanto de la lorenca grupo agas sur la ĉiela sfero laŭ la sama maniero kiel la möbius-a grupo agas sur la rimana sfero. Fakte, ĉi tiuj du grupoj estas izomorfaj. Rigardanto kiu akcelas al relativisma rapideco vidos kiel la ŝablono de konstelacioj proksime al la Tero kontinue transformiĝas laŭ infinitezimaj möbius-aj transformoj. Ĉi tiu observado estas ofte prenita kiel la deirpunkto de twistor-teorio.

Difino

La ĝenerala formo de transformo de Möbius estas donita per

$z\mapsto \frac{az+b}{cz+d}$

kie a, b, c, d estas kompleksaj nombroj tiuj ke ad − _bc_ ≠ 0. Ĉi tiu difino povas esti etendita al la tuta Rimana sfero (la kompleksa ebeno plus la punkto je malfinio) kun du specialaj okazoj:

• la punkto $z=-d/c$ estas mapita al $\mathrm{\infty }$
• la punkto $z=\mathrm{\infty }$ estas mapita al $a/c$

Oni povas havi Möbius-ajn transformojn por la reelaj nombroj kaj ankaŭ por la kompleksaj nombroj. En ambaŭ okazoj, oni bezonas pligrandigi la domajnon per punkto je malfinio.

La kondiĉo ad − bc ≠ 0 asekuras ke la transformo estas inversigebla). La inversa transformo estas donita per

$z\mapsto \frac{dz-b}{-cz+a}$

kun la samaj specialaj okazoj.

La aro de ĉiuj möbius-aj transformoj formas grupon sub komponaĵo. Ĉi tiu grupo povas esti strukturita kiel kompleksa dukto, kie komponaĵo kaj inversigo estas holomorfaj mapoj. La möbius-a grupo estas tiam komplekso Lie-grupo. Ĝi estas kutime signita $\text{Aut}(\widehat{ℂ})$, ĉar ĝi estas la aŭtomorfia grupo de la Rimana sfero.

Projekciaj matricaj prezentoj

La transformo

$f(z)=\frac{az+b}{cz+d}$

povas esti utile esprimita kiel matrico

$ℌ=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right).$

La kondiĉo anonco − _bc_ ≠ 0 estas ekvivalento al la kondiĉo (tiu, ke, kiu) la determinanto de pli supre matrico esti nenulo (kio estas la matrico devus esti ne-singularo). (Tononomo, Noto, Noti) (tiu, ke, kiu) multiplikante $ℌ$ per (ĉiu, iu) kompleksa nombro λ donas pligrandiĝo al la sama transformo. Tiaj matricaj prezentoj estas (nomita, vokis) projekciaj prezentoj por kaŭzoj eksplikis pli sube. Ĝi estas ofte oportuna al ununormigi $ℌ$ por ke ĝia determinanto estas egala al 1. La matrico $ℌ$ estas tiam unika supren al signo.

La utileco de ĉi tiu prezento estas (tiu, ke, kiu) la komponaĵo de du Möbius-a (transformoj, transformas) korespondas precize al matrica multipliko de la korespondantaj matricoj. Tio estas, se ni difini mapo

$\pi :\text{GL}(2,ℂ)\to \text{Aut}(\widehat{ℂ})$

de la ĝenerala lineara grupo Gl(2,C) al la Möbius-a grupo kiu sendas la matrico $ℌ$ al la transformo f, tiam ĉi tiu mapo estas grupa homomorfio.

La mapo $\pi$ estas ne izomorfio, ekde ĝi (mapoj, mapas) (ĉiu, iu) skalaro multaj de $ℌ$ al la sama transformo. La kerno de ĉi tiu homomorfio estas tiam la aro de ĉiuj skalaraj matricoj Z(2,C). La kvocienta grupo Gl(2,C)/Z(2,C) estas (nomita, vokis) la projekcia lineara grupo kaj estas kutime signifita _PGL_(2,C). Per la unua izomorfia teoremo de grupa teorio ni konkludi (tiu, ke, kiu) la Möbius-a grupo estas izomorfia al _PGL_(2,C). Ankaŭ, la natura ago de _PGL_(2,C) sur la kompleksa projekcia linio _CP_¹ estas akurate la natura ago de la Möbius-a grupo sur la Rimana sfero kiam la sfero kaj la projekcia linio estas (identigita, identigita) kiel sekvas:

$[z_1:z_2]\leftrightarrow z_1/z_2.$

Ĉi tie [z₁:z₂] estas homogenaj koordinatoj sur _CP_¹.

Se unu ununormigas $ℌ$ por ke la determinanto estas egala al unu, la mapo $\pi$ limigas al (surjekcia, surĵeta) mapo de la speciala lineara grupo _SL_(2,C) al la Möbius-a grupo. La Möbius-a grupo estas pro tio ankaŭ izomorfia al _PSL_(2,C). Ni tiam havi jeno (izomorfioj, izomorfias):

$\text{Aut}(\widehat{ℂ})\cong \text{PGL}(2,ℂ)\cong \text{PSL}(2,ℂ).$

De la lasta identigo ni vidi (tiu, ke, kiu) la Möbius-a grupo estas 3-dimensia komplekso (Mensogi, Kuŝi) grupo (aŭ 6-dimensia (reala, reela) (Mensogi, Kuŝi) grupo).

(Tononomo, Noto, Noti) (tiu, ke, kiu) estas precize du matrica unuhava determinanto kiu povas kutimi prezenti (ĉiu, iu) donita Transformo de Möbius. Tio estas, _SL_(2,C) estas duopa kovri de _PSL_(2,C). Ekde _SL_(2,C) estas simple-koneksa ĝi estas la universala kovri de la Möbius-a grupo. La fundamenta grupo de la Möbius-a grupo estas tiam Z₂.

Propraĵoj

(Ĉiu, Iu) Transformo de Möbius povas esti (verkita, komponita) de la rudimenta (transformoj, transformas): _dilations_, (tradukoj, tradukas, translacioj, translacias) kaj (renversaĵoj, renversaĵas, inversigoj, inversigas). Se ni difini linio al esti cirklo (trairanta, pasanta) tra malfinio, tiam ĝi povas esti montrita (tiu, ke, kiu) Transformo de Möbius (mapoj, mapas) cirkloj al cirkloj, per (aspektanta, rigardanta) je ĉiu rudimenta transformo.

La kruci-rilata konservada teoremo ŝtatoj (tiu, ke, kiu) la kruci-rilato

$\frac{(z_1-z_3)(z_2-z_4)}{(z_1-z_4)(z_2-z_3)}=\frac{(w_1-w_3)(w_2-w_4)}{(w_1-w_4)(w_2-w_3)}$

estas invarianto sub Transformo de Möbius (tiu, ke, kiu) (mapoj, mapas) de z al w.

La ago de la Möbius-a grupo sur la Rimana sfero estas akre 3-transitiva en la senco ke tiu estas unika Transformo de Möbius kiu prenas ĉiujn tri klarajn punktojn sur la Rimana sfero al ĉiu alia aro de tri klaraj punktoj. Vidi la sekcio pli sube sur preciziganta transformo per tri punktoj.

Klasifiko

Möbius-a (transformoj, transformas) estas kutime (klasifikita, klasigita) enen kvar (klavas, tipoj), parabola, elipsa, hiperbola kaj _loxodromic_ (reale hiperbola estas speciala okazo de _loxodromic_). La klasifiko havas ambaŭ algebra kaj geometria signifeco. Geometrie, la malsama (klavas, tipoj) rezulto en malsama (transformoj, transformas) de la kompleksa ebeno, kiel la (ciferoj, ciferas, geometriaj figuroj, figuroj, figuras) pli sube ilustri. Ĉi tiuj (klavas, tipoj) povas esti (distingita, invarianta, memkonjugita, normala, diferencigis) per (aspektanta, rigardanta) je la spuro $\text{tr}ℌ=a+d$. (Tononomo, Noto, Noti) (tiu, ke, kiu) la spuro estas invarianto sub konjugo, tio estas,

$\text{tr}{𝔊ℌ𝔊}^{-1}=\text{tr}ℌ$

kaj (do, tiel) ĉiu membro de _conjugacy_ klaso estos havi la sama spuro. Ĉiu Transformo de Möbius povas esti skribita tia (tiu, ke, kiu) ĝia (figuranta, prezentanta) matrico $ℌ$ havas determinanto unu (per multiplikante la elementoj kun taŭgi skalaro). Du Möbius-a (transformoj, transformas) $ℌ,{ℌ}^{\prime }$ (ambaŭ ne egala al la idento (konverti, konverto)) kun $\det ℌ=\det {ℌ}^{\prime }=1$ estas konjugita se kaj nur se ${\text{tr}}^2ℌ={\text{tr}}^2{ℌ}^{\prime }$.

En jena diskuto ni estos ĉiam alpreni (tiu, ke, kiu) la (figuranta, prezentanta) matrico $ℌ$ estas ununormigita tia (tiu, ke, kiu) $\det ℌ=ad-bc=1$.

Parabola (konvertas, konvertoj) La (konverti, konverto) estas dirita al esti parabola se

${\text{tr}}^2ℌ=(a+d{)}^2=4$.

(Konverti, Konverto) estas parabola se kaj nur se ĝi havas unu fiksa punkto en la _compactified_ kompleksa ebeno $\widehat{ℂ}=ℂ\cup \{\mathrm{\infty }\}$. Ĝi estas parabola se kaj nur se ĝi estas konjugita al

$\left(\begin{array}{cc}1& 1\\ 0& 1\end{array}\right)$.

La subgrupo de parabola (konvertas, konvertoj) estas ekzemplo de Borela subgrupo, kiu ĝeneraligas la ideo al pli altaj dimensioj.

Ĉiu alia ne-idento (transformoj, transformas) havi du fiksaj punktoj. Ĉiuj ne-parabola (ne-idento) (konvertas, konvertoj) estas konjugita al

$\left(\begin{array}{cc}\lambda & 0\\ 0& {\lambda }^{-1}\end{array}\right)$

kun $\lambda$ ne egala al 0,1 aŭ -1. La kvadrato $k={\lambda }^2$ estas (nomita, vokis) la karakteriza konstanto aŭ multiplikanto de la transformo.

Elipsa (konvertas, konvertoj) La (konverti, konverto) estas dirita al esti elipsa se

$0\le {\text{tr}}^2ℌ<4$.

(Konverti, Konverto) estas elipsa se kaj nur se $|\lambda |=1$. Skribanta $\lambda =e^{i\alpha }$, elipsa (konverti, konverto) estas konjugita al

$\left(\begin{array}{cc}\cos \alpha & \sin \alpha \\ -\sin \alpha & \cos \alpha \end{array}\right)$

kun $\alpha$ (reala, reela). (Tononomo, Noto, Noti) (tiu, ke, kiu) por (ĉiu, iu) $ℌ$, la karakteriza konstanto de ${ℌ}^n$ estas $k^n$. Tial, la nur Möbius-a (transformoj, transformas) de finia (mendi, ordo) estas la elipsa (transformoj, transformas), kaj ĉi tiuj nur kiam λ estas radiko de unueco; ekvivalente, kiam α estas (racionala, racionalo) multaj de pi.

Hiperbola (konvertas, konvertoj) La (konverti, konverto) estas dirita al esti hiperbola se

${\text{tr}}^2ℌ>4$.

(Konverti, Konverto) estas hiperbola se kaj nur se λ estas (reala, reela) kaj pozitiva.

_Loxodromic_ (konvertas, konvertoj) La (konverti, konverto) estas dirita al esti _loxodromic_ se ${\text{tr}}^2ℌ$ estas ne en la segmento de [0,4]. Hiperbola (konvertas, konvertoj) estas tial speciala okazo de _loxodromic_ (transformoj, transformas). Transformo estas _loxodromic_ se kaj nur se $|\lambda |\ne 1$. Historie, navigado per _loxodrome_ aŭ _rhumb_ linio (ligas, referas) al vojo de konstanto (ursanta, lagro); la rezultanta vojo estas logaritma spiralo, simila en formo al la (transformoj, transformas) de la kompleksa ebeno (tiu, ke, kiu) _loxodromic_ Transformo de Möbius (konstruas, faras). Vidi la geometria (ciferoj, ciferas, geometriaj figuroj, figuroj, figuras) pli sube.

Transformo	Spuro (kvadratis, placita, kvadratigita)	(Multiplikantoj, Multiplikantas)	Klasa prezentanto
Elipsa	$0\le \sigma <4$	$|k|=1$ $k=e^{\pm i\theta }\ne 1$	$\left(\begin{array}{cc}{e}^{i\theta /2}& 0\\ 0& e^{-i\theta /2}\end{array}\right)$	$z\mapsto e^{i\theta }z$
Parabola	$\sigma =4$	$k=1$	$\left(\begin{array}{cc}1& a\\ 0& 1\end{array}\right)$	$z\mapsto z+a$
Hiperbola	$4<\sigma <\mathrm{\infty }$	$k\in {ℝ}^{+}$ $k=e^{\pm \theta }\ne 1$	$\left(\begin{array}{cc}{e}^{\theta /2}& 0\\ 0& e^{-\theta /2}\end{array}\right)$	$z\mapsto e^{\theta }z$
_Loxodromic_	$\sigma \in ℂ,\sigma \in ̸[0,4]$	$|k|\ne 1$ $k={\lambda }^2,{\lambda }^{-2}$	$\left(\begin{array}{cc}\lambda & 0\\ 0& {\lambda }^{-1}\end{array}\right)$	$z\mapsto kz$

Fiksaj punktoj

Ĉiu ne-identa Transformo de Möbius havas du fiksaj punktoj ${\gamma }_1,{\gamma }_2$ sur la Rimana sfero. (Tononomo, Noto, Noti) (tiu, ke, kiu) la fiksaj punktoj estas grafita ĉi tie kun obleco; por parabola (transformoj, transformas), la fiksaj punktoj koincidi. Ĉu aŭ ambaŭ de ĉi tiuj fiksaj punktoj (majo, povas) esti la punkto je malfinio.

La fiksaj punktoj de la transformo

$f(z)=\frac{az+b}{cz+d}$

estas ricevita per solvanta la fiksa punkta ekvacio $f(\gamma )=\gamma$. Por $c\ne 0$, ĉi tiu havas du (radikoj, radikas) (pruvo):

${\gamma }_{1,2}=\frac{(a-d)\pm \sqrt{(a-d{)}^2+4bc}}{2c}=\frac{(a-d)\pm \sqrt{(a+d{)}^2-4(ad-bc)}}{2c}.$

(Tononomo, Noto, Noti) (tiu, ke, kiu) por parabola (transformoj, transformas), kiu kontentigi $(a+d{)}^2=4(ad-bc)$, la fiksaj punktoj koincidi.

Kiam $c=0$ unu de la fiksaj punktoj estas je malfinio, la alia estas donita per

$\gamma =-\frac{b}{a-d}.$

La transformo estos esti simpla transformo (verkis, komponita) de (tradukoj, tradukas, translacioj, translacias), (rotacioj, rotacias), kaj _dilations_: $z\mapsto \alpha z+\beta$.

Se $c=0$ kaj $a=d$, tiam ambaŭ fiksaj punktoj estas je malfinio, kaj la Transformo de Möbius korespondas al pura traduko: $z\mapsto z+\beta$.

Normala formo

Möbius-a (transformoj, transformas) estas ankaŭ iam skribita en (termoj, kondiĉoj, terminoj, termas, terminas) de iliaj fiksaj punktoj en (do, tiel)-(nomita, vokis) normala formo. Ni unua (trakti, kuraci) la ne-parabola (kesto, okazo), por kiu estas du klaraj fiksaj punktoj.

Ne-parabola (kesto, okazo):

Ĉiu ne-parabola transformo estas konjugita al _dilation_, kio estas transformo de la (formo, formi)

$z\mapsto kz$

kun fiksaj punktoj je 0 kaj ∞. Al vidi ĉi tiu difini mapo

$g(z)=\frac{z-{\gamma }_1}{z-{\gamma }_2}$

kiu sendas la punktoj $({\gamma }_1,{\gamma }_2)$ al $(0,\mathrm{\infty })$. Ĉi tie ni alpreni (tiu, ke, kiu) ambaŭ ${\gamma }_1$ kaj ${\gamma }_2$ estas finia. Se unu de ilin estas jam je malfinio tiam g povas esti aliigita (do, tiel) rilate (fiksi, neŝanĝebligi) malfinio kaj sendi la alia punkto al 0.

Se f havas klaraj fiksaj punktoj $({\gamma }_1,{\gamma }_2)$ tiam la transformo $gf{g}^{-1}$ havas fiksaj punktoj je 0 kaj ∞ kaj estas pro tio _dilation_: $gf{g}^{-1}(z)=kz$. La fiksa punkta ekvacio por la transformo f povas tiam esti skribita

$\frac{f(z)-{\gamma }_1}{f(z)-{\gamma }_2}=k\frac{z-{\gamma }_1}{z-{\gamma }_2}.$

Solvanta por f donas (en matrico (formo, formi)):

$ℌ(k;{\gamma }_1,{\gamma }_2)=\left(\begin{array}{cc}{\gamma }_1-k{\gamma }_2& (k-1){\gamma }_1{\gamma }_2\\ 1-k& k{\gamma }_1-{\gamma }_2\end{array}\right)$

aŭ, se unu de la fiksaj punktoj estas je malfinio:

$ℌ(k;\gamma ,\mathrm{\infty })=\left(\begin{array}{cc}k& (1-k)\gamma \\ 0& 1\end{array}\right)$

De la pli supre esprimoj unu povas kalkuli la derivaĵoj de f je la fiksaj punktoj:

$f^{\prime }({\gamma }_1)=k$ kaj $f^{\prime }({\gamma }_2)=1/k.$

Observi (tiu, ke, kiu), donita (ordenanta, mendanta, ordanta, dimensianta, komandanta, ordigo) de la fiksaj punktoj, ni povas (distingi, diferencigi) unu de la (multiplikantoj, multiplikantas) (k) de f kiel la karakteriza konstanto de f. Dorsflankanta la (mendi, ordo) de la fiksaj punktoj estas ekvivalento al prenante la inversa multiplikanto por la karakteriza konstanto:

$ℌ(k;{\gamma }_1,{\gamma }_2)=ℌ(1/k;{\gamma }_2,{\gamma }_1).$

Por _loxodromic_ (transformoj, transformas), ĉiam $|k|>1$, unu diras (tiu, ke, kiu) ${\gamma }_1$ estas la forloga fiksa punkto, kaj ${\gamma }_2$ estas la alloga fiksa punkto. Por $|k|<1$, la (roloj, rolas) estas dorsflankita.

Parabola (kesto, okazo):

En la parabola (kesto, okazo) estas nur unu fiksa punkto $\gamma$. La transforma sendanta punkto al ∞ estas

$g(z)=\frac{1}{z-\gamma }$

aŭ la idento se $\gamma$ estas jam je malfinio. La transformo $gf{g}^{-1}$ _fixes_ malfinio kaj estas pro tia traduko:

$gf{g}^{-1}(z)=z+\beta .$

Ĉi tie, β estas (nomita, vokis) la traduka longo. La fiksa punkta formulo por parabola transformo estas tiam

$\frac{1}{f(z)-\gamma }=\frac{1}{z-\gamma }+\beta$.

Solvanta por f (en matrico (formo, formi)) donas

$ℌ(\beta ;\gamma )=\left(\begin{array}{cc}1+\gamma \beta & -\beta {\gamma }^2\\ \beta & 1-\gamma \beta \end{array}\right)$

aŭ, se $\gamma =\mathrm{\infty }$:

$ℌ(\beta ;\mathrm{\infty })=\left(\begin{array}{cc}1& \beta \\ 0& 1\end{array}\right)$

(Tononomo, Noto, Noti) (tiu, ke, kiu) $\beta$ estas ne la karakteriza konstanto de f, kiu estas ĉiam 1 por parabola transformo. De la pli supre esprimoj unu povas kalkuli:

$f^{\prime }(\gamma )=1.$

Geometria interpretado de la karakteriza konstanto

Jena bildo prezentas (post _stereographic_ transformo de la sfero al la ebeno) la du fiksaj punktoj de Transformo de Möbius en la ne-parabola (kesto, okazo):

Image:Mobius_Identity.jpeg

La karakteriza konstanto povas esti esprimita en (termoj, kondiĉoj, terminoj, termas, terminas) de ĝia logaritmo:

$e^{\rho +\alpha i}=k$

Kiam esprimita en tiamaniere, la reela nombro $\rho$ iĝas elvolvaĵa faktoro. Ĝi indikas kiel forloga la fiksa punkto ${\gamma }_1$ estas, kaj kiel alloga ${\gamma }_2$ estas. La reela nombro $\alpha$ estas rotacia faktoro, indikanta kiagrade la (konverti, konverto) turnas la ebeno kontraŭ-dekstrume pri ${\gamma }_1$ kaj dekstrume pri ${\gamma }_2$.

Elipsa (transformoj, transformas)

Se $\rho =0$, tiam la fiksaj punktoj estas neniu alloga nek forloga sed indiferenta, kaj la transformo estas dirita al esti _elliptical_. Ĉi tiuj (transformoj, transformas) flegi movi ĉiuj punktoj en cirkloj ĉirkaŭ la du fiksaj punktoj. Se unu de la fiksaj punktoj estas je malfinio, ĉi tiu estas ekvivalento al farante afina rotacio ĉirkaŭ punkto.

Se ni preni la unu-parametra subgrupo generita per (ĉiu, iu) elipsa Transformo de Möbius, ni ricevi kontinua transformo, tia (tiu, ke, kiu) ĉiu transformo en la subgrupo _fixes_ la sama du punktoj. Ĉiuj aliaj punktoj (flui, fluo) laŭ familio de cirkloj kiu estas (nestita, nestis) inter la du fiksaj punktoj sur la Rimana sfero. En ĝenerala, la du fiksaj punktoj povas esti (ĉiu, iu) du klaraj punktoj.

Ĉi tiu havas grava fizika interpretado. Imagi (tiu, ke, kiu) iu rigardanto turnas kun konstanta akraflanka rapido pri iu akso. Tiam ni povas preni la du fiksaj punktoj al esti la Nordo kaj Sudo (polusoj, polusas) de la ĉiela sfero. La (aper(aĵ)o, aspekto) de la nokta ĉielo estas nun konvertis kontinue en akurate la maniero priskribis per la unu-parametra subgrupo de elipsa (transformoj, transformas) (kotizanta, kvotanta, akcianta, komuniganta, partanta) la fiksaj punktoj $0,\mathrm{\infty }$, kaj kun la nombro $\alpha$ korespondanta al la konstanta akraflanka rapido de nia rigardanto.

Jen iu (ciferoj, ciferas, geometriaj figuroj, figuroj, figuras) ilustranta la efiki de elipsa Transformo de Möbius sur la Rimana sfero (post _stereographic_ projekcio al la ebeno):

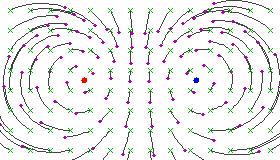	Image:Mobius_Large_Neg_Elliptical.jpeg
Image:Mobius_Small_Pos_Elliptical.jpeg	Image:Mobius_Large_Pos_Elliptical.jpeg

Ĉi tiuj (bildoj, bildas) ilustri la efiki de sola Transformo de Möbius. La unu-parametra subgrupa kiu ĝi (generas, naskas) kontinue movas punktoj laŭ la familio de cirkulero (arkoj, arkas, eĝoj, eĝas) sugestita per la (bildoj, bildas).

Hiperbola (transformoj, transformas)

Se $\alpha$ estas nulo (aŭ multaj de $2\pi$), tiam la transformo estas dirita al esti hiperbola. Ĉi tiuj (transformoj, transformas) flegi movi punktoj laŭ cirkuleraj vojoj de unu fiksa punkto al la alia.

Se ni preni la unu-parametra subgrupo generita per (ĉiu, iu) hiperbola Transformo de Möbius, ni ricevi kontinua transformo, tia (tiu, ke, kiu) ĉiu transformo en la subgrupo _fixes_ la sama du punktoj. Ĉiuj aliaj punktoj (flui, fluo) laŭ certa familio de cirkulero (arkoj, arkas, eĝoj, eĝas) for de la unua fiksa punkto kaj al la (sekundo, dua) fiksa punkto. En ĝenerala, la du fiksaj punktoj (majo, povas) esti (ĉiu, iu) du klaraj punktoj sur la Rimana sfero.

Ĉi tiu ankaŭ havas grava fizika interpretado. Imagi (tiu, ke, kiu) rigardanto akcelas (kun konstanta grandeco de akcelo) direkte al la Norda poluso sur lia ĉiela sfero. Tiam la (aper(aĵ)o, aspekto) de la nokta ĉielo estas konvertita en akurate la maniero priskribis per la unu-parametra subgrupo de hiperbola (transformoj, transformas) (kotizanta, kvotanta, akcianta, komuniganta, partanta) la fiksaj punktoj $0,\mathrm{\infty }$, kun la reela nombro $\rho$ korespondanta al la grandeco de lia akcela vektoro. La (steloj, astroj) aspekti al movi laŭ (longitudoj, longitudas), for de la Suda poluso al la Norda poluso. (La (longitudoj, longitudas) aperi kiel cirkulero (arkoj, arkas, eĝoj, eĝas) sub _stereographic_ projekcio de la sfero al la ebeno).

Jen iu (ciferoj, ciferas, geometriaj figuroj, figuroj, figuras) ilustranta la efiki de hiperbola Transformo de Möbius sur la Rimana sfero (post _stereographic_ projekcio al la ebeno):

	Image:Mobius_Large_Neg_Hyperbolic.jpeg
Image:Mobius_Small_Pos_Hyperbolic.jpeg

Ĝi estas ne surprizanta (tiu, ke, kiu) ĉi tiuj (bildoj, bildas) (aspekti, aspekto, rigardi) treege ŝati la kampaj linioj de (mezuro, drinkejo, bari) (magnetoj, magnetas), ekde la cirkulero (flui, fluo) linioj substreĉi konstanta angulo inter la du fiksaj punktoj.

_Loxodromic_ (transformoj, transformas)

Se ambaŭ ρ kaj α estas nenulo, tiam la transformo estas dirita al esti _loxodromic_. Ĉi tiuj (transformoj, transformas) flegi movi ĉiuj punktoj en S-formis vojoj de unu fiksa punkto al la alia.

La vorto "_loxodrome_" estas de la Greko: "_loxos_, oblikvanta + _dromos_, kurso". Kiam velanta sur konstanto (ursanta, lagro) - se vi flegi (kapanta, kapetanta, kranianta, rubriko) de (diri) nordo-oriento, vi estos eble hisi velanta ĉirkaŭ la norda poluso en logaritma spiralo. Sur la _mercator_ projekcia tia kurso estas rekto, kiel la nordo kaj sudo (polusoj, polusas) (projekcii, projekto) al malfinio. La angulo (tiu, ke, kiu) la _loxodrome_ substreĉas relativa al la linioj de longitudo (ie, ĝia inklino, la "_tightness_" de la spiralo) estas la argumento de k. Kompreneble, Möbius-a (transformoj, transformas) (majo, povas) havi ilia du fiksaj punktoj ie, ne (justa, ĵus) je la nordo kaj sudo (polusoj, polusas). Sed (ĉiu, iu) _loxodromic_ transformo estos esti konjugita al (konverti, konverto) (tiu, ke, kiu) movas ĉiuj punktoj laŭ tia _loxodromes_.

Se ni preni la unu-parametra subgrupo generita per (ĉiu, iu) _loxodromic_ Transformo de Möbius, ni ricevi kontinua transformo, tia (tiu, ke, kiu) ĉiu transformo en la subgrupo _fixes_ la sama du punktoj. Ĉiuj aliaj punktoj (flui, fluo) laŭ certa familio de kurboj, for de la unua fiksa punkto kaj al la (sekundo, dua) fiksa punkto. Malverŝajne la hiperbola (kesto, okazo), ĉi tiuj kurboj estas ne cirkulero (arkoj, arkas, eĝoj, eĝas), sed certaj kurboj kiu sub _stereographic_ projekcio de la sfero al la ebeno aperi kiel spiralaj kurboj kiu tordi kontraŭhorloĝnadla malfinie ofte ĉirkaŭ unu fiksa punkto kaj tordi dekstrume malfinie ofte ĉirkaŭ la alia fiksa punkto. En ĝenerala, la du fiksaj punktoj (majo, povas) esti (ĉiu, iu) du klaraj punktoj sur la Rimana sfero.

Vi povas kredeble konjekti, ke la fizika interpretado en la kazo, kiam la du fiksaj punktoj estas $0,\mathrm{\infty }$: rigardanto kiu estas ambaŭ turnanta (kun konstanta akraflanka rapido) pri iu akso kaj kun konstanta grandeco akceliĝas laŭ la sama akso, estos vidi la aperaĵon de la nokta ĉielo transformita laŭ la unu-parametra subgrupo de loksodromiaj transformoj kun fiksaj punktoj $0,\mathrm{\infty }$, kaj kun $\rho ,\alpha$ difinita respektive per la grandeco de akcelo kaj akraflanka rapido.

Jen iuj bildoj ilustrantaj la efikoj de loksodromia transformo:

Image:Mobius_Small_Loxodromic.jpeg

Image:Mobius_Large_Loxodromic.jpeg

Stereografia projekcio

Ĉi tiuj bildoj montri Möbius-a (transformoj, transformas) _stereographically_ (projekciis, projektita) sur la Rimana sfero. (Tononomo, Noto, Noti) en aparta (tiu, ke, kiu) kiam (projekciis, projektita) sur sfero, la speciala okazo de fiksa punkto je malfinio (aspektas, aspektoj, rigardas) ne malsama al havanta la fiksaj punktoj en ajna loko.

	Elipsa	Hiperbola	_Loxodromic_
Unu fiksa punkto je Malfinio		Image:Mob3d-hyp-inf-200.png
Fiksaj punktoj _diametrically_ kontraŭa	Image:Mob3d-elip-opp-200.png	Image:Mob3d-hyp-opp-200.png
Fiksaj punktoj en ajna loko	Image:Mob3d-elip-arb-200.png	Image:Mob3d-hyp-arb-200.png	Image:Mob3d-lox-arb-200.png

Ripetanta transformo

Se transformo $ℌ$ havas fiksaj punktoj ${\gamma }_1,{\gamma }_2$, kaj karakteriza konstanto 'k, tiam ${ℌ}^{\prime }={ℌ}^n$ estos havi ${{\gamma }_1}^{\prime }={\gamma }_1,{{\gamma }_2}^{\prime }={\gamma }_2,k^{\prime }=k^n$.

Ĉi tiu povas kutimi ripeti transformo, aŭ al animi unu per rompanta ĝi supren enen (ŝtupoj, ŝtupas, paŝas).

Ĉi tiuj bildoj montri tri punktoj ((ruĝa, legita), blua kaj nigra) kontinue ripetis sub (transformoj, transformas) kun diversa karakterizo (konstantoj, konstantas).

Image:Mobius23623.jpeg	Image:Mobius23624.jpeg
Image:Mobius23625.jpeg

Simila koncepto estas la krajono de transformoj, kie la transformoj estas parametrigitaj kaj formas kontinuon.

Malfiniigantoj de la transformo

La punkto

$z_{\mathrm{\infty }}=-\frac{d}{c}$

estas la malfiniiganto de $ℌ$; ĉe tiu punkto, la valoroj de $ℌ(z)=\frac{az+b}{cz+d}$ estas mallime grandaj.

La inversa malfiniiganto

$Z_{\mathrm{\infty }}=\frac{a}{c}$

estas la punkto al kiu la punkto je malfinio estas bildigata. La punkto _midway_ inter la du (polusoj, polusas) estas ĉiam la sama kiel la punkto _midway_ inter la du fiksaj punktoj:

${\gamma }_1+{\gamma }_2=z_{\mathrm{\infty }}+Z_{\mathrm{\infty }}$

Ĉi tiuj kvar punktoj estas verticoj de paralelogramo kiu estas kelkfoje nomata la karakteriza paralelogramo de la transformo.

(Konverti, Konverto) $ℌ$ povas esti precizigita kun du fiksaj punktoj ${\gamma }_1,{\gamma }_2$ kaj la poluso $z_{\mathrm{\infty }}$.

$ℌ=\left(\begin{array}{cc}{Z}_{\mathrm{\infty }}& -{\gamma }_1{\gamma }_2\\ 1& -z_{\mathrm{\infty }}\end{array}\right),Z_{\mathrm{\infty }}={\gamma }_1+{\gamma }_2-z_{\mathrm{\infty }}$

Ĉi tiu permesas al ni derivi formulo por konvertiĝo inter $k$ kaj $z_{\mathrm{\infty }}$ donita ${\gamma }_1,{\gamma }_2$:

$z_{\mathrm{\infty }}=\frac{k{\gamma }_1-{\gamma }_2}{1-k}$

$k=\frac{{\gamma }_2-z_{\mathrm{\infty }}}{{\gamma }_1-z_{\mathrm{\infty }}}=\frac{Z_{\mathrm{\infty }}-{\gamma }_1}{Z_{\mathrm{\infty }}-{\gamma }_2}=\frac{a-c{\gamma }_1}{a-c{\gamma }_2}$

Kiu reduktas lanugo al

$k=\frac{(a+d)+\sqrt{(a-d{)}^2+4bc}}{(a+d)-\sqrt{(a-d{)}^2+4bc}}$

La lasta esprimo koincidas kun unu de la (reciproke (reciproka, reciprokaĵo, inverso)) ajgeno (rilatoj, rilatas, kvocientoj, kvocientas) $\frac{{\lambda }_1}{{\lambda }_2}$ de la matrico

$ℌ=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$

(figuranta, prezentanta) la (konverti, konverto) (kompari la diskuto en la antaŭvenanta sekcio pri la karakteriza konstanto de transformo). Ĝia karakteriza polinomo estas egala al

$\text{det}(\lambda I_2-ℌ)={\lambda }^2-\text{tr}ℌ\lambda +\text{det}ℌ={\lambda }^2-(a+d)\lambda +(ad-bc)$

kiu havas (radikoj, radikas)

${\lambda }_i=\frac{(a+d)\pm \sqrt{(a-d{)}^2+4bc}}{2}=\frac{(a+d)\pm \sqrt{(a+d{)}^2-4(ad-bc)}}{2}.$

Preciziganta transformo per tri punktoj

Proksimumo per rekta maniero

Ĉiu aro de tri punktoj

$Z_1=ℌ(z_1),Z_2=ℌ(z_2),Z_3=ℌ(z_3)$

unike difinas transformon $ℌ$. Por kalkuli ĉi tiun eksteren, estas oportune utiligi transformon, tio estas per ebeno kun tri punktoj sur (0,0), (1, 0) kaj la punkto je malfinio.

${ℌ}_1=\left(\begin{array}{cc}\frac{z_2-z_3}{z_2-z_1}& -z_1\frac{z_2-z_3}{z_2-z_1}\\ 1& -z_3\end{array}\right),{ℌ}_2=\left(\begin{array}{cc}\frac{Z_2-Z_3}{Z_2-Z_1}& -Z_1\frac{Z_2-Z_3}{Z_2-Z_1}\\ 1& -Z_3\end{array}\right)$

Unu povas forigi la (infinitoj, infinitas, malfinioj, malfinias, nefinioj, nefinias) per multiplikante ekster per $z_2-z_1$ kaj $Z_2-Z_1$ kiel antaŭe (tononomis, notita).

${ℌ}_1=\left(\begin{array}{cc}{z}_2-z_3& z_1{z}_3-z_1{z}_2\\ z_2-z_1& z_1{z}_3-z_3{z}_2\end{array}\right),{ℌ}_2=\left(\begin{array}{cc}{Z}_2-Z_3& Z_1{Z}_3-Z_1{Z}_2\\ Z_2-Z_1& Z_1{Z}_3-Z_3{Z}_2\end{array}\right)$

La matrico $ℌ$ al mapo $z_{1,2,3}$ sur $Z_{1,2,3}$ tiam iĝas

$ℌ={ℌ}_2^{-1}{ℌ}_1$

Vi povas multipliki ĉi tiu ekster, se vi bezono, sed se vi estas skribanta kodo tiam ĝi's pli simpla al uzi nedaŭra (variabloj, variablas) por la mezo (termoj, kondiĉoj, terminoj, termas, terminas).

Eksplicita determinanta formulo

La problemo de konstruanta Transformo de Möbius $ℌ(z)$ (mapanta, bildigo) triopo $(z_1,z_2,z_3)$ al alia triopo $(w_1,w_2,w_3)$ estas ekvivalento al trovanta la ekvacio de norma hiperbolo

$cwz-az+dw-b=0$

en la (z,w)-ebeno (trairanta, pasanta) tra la punktoj $(z_i,w_i)$. Eksplicita ekvacio povas troviĝi per pritaksanta la determinanto

$\det \left(\begin{array}{cccc}zw& z& w& 1\\ z_1{w}_1& z_1& w_1& 1\\ z_2{w}_2& z_2& w_2& 1\\ z_3{w}_3& z_3& w_3& 1\end{array}\right)$

per Laplaca elvolvaĵo laŭ la unua (linio, vico). Ĉi tiuj rezultoj en la determinantaj formuloj

$a=\det \left(\begin{array}{ccc}{z}_1{w}_1& w_1& 1\\ z_2{w}_2& w_2& 1\\ z_3{w}_3& w_3& 1\end{array}\right)$

$b=\det \left(\begin{array}{ccc}{z}_1{w}_1& z_1& w_1\\ z_2{w}_2& z_2& w_2\\ z_3{w}_3& z_3& w_3\end{array}\right)$

$c=\det \left(\begin{array}{ccc}{z}_1& w_1& 1\\ z_2& w_2& 1\\ z_3& w_3& 1\end{array}\right)$

$d=\det \left(\begin{array}{ccc}{z}_1{w}_1& z_1& 1\\ z_2{w}_2& z_2& 1\\ z_3{w}_3& z_3& 1\end{array}\right)$

por la koeficientoj $a,b,c,d$ de la (figuranta, prezentanta) matrico $ℌ=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)$. La konstruis matrico $ℌ$ havas determinanto egala al $(z_1-z_2)(z_1-z_3)(z_2-z_3)(w_1-w_2)(w_1-w_3)(w_2-w_3)$ kiu ne nuliĝi se la z_mi _resp_. w_mi estas duoplarĝa malsama tial la Transformo de Möbius estas bone-difinita.

Mallaŭdo: A simila determinanto (kun $wz$ (anstataŭigita, anstataŭigis) per $w^2+z^2$) (plumboj, plumbas, kondukas) al la ekvacio de cirklo tra tri malsama (ne samrekta) punktoj en la ebeno.

Cetera maniero uzante kruci-rilatojn de kvar punktoj

Ĉi tiu konstruado ekspluatas la fakton (menciitan en la unua sekcio), ke la kruci-rilato

$\text{cr}(z_1,z_2,z_3,z_4)=\frac{(z_1-z_3)(z_2-z_4)}{(z_1-z_4)(z_2-z_3)}$

estas invarianto sub Transformo de Möbius (mapanta, bildigo) kvaropo $(z_1,z_2,z_3,z_4)$ al $(w_1,w_2,w_3,w_4)$ tra $w_i=ℌz_i$. Se $ℌ$ (mapoj, mapas) triopo $(z_1,z_2,z_3)$ de duoplarĝa malsama z_mi al alia triopo $(w_1,w_2,w_3)$, tiam la Transformo de Möbius $ℌ$ estas difinita per la ekvacio

$\text{cr}(ℌ(z),w_1,w_2,w_3)=\text{cr}(z,z_1,z_2,z_3)$

aŭ skribita ekster en (betono, konkreta) (termoj, kondiĉoj, terminoj, termas, terminas):

$\frac{(ℌ(z)-w_2)(w_1-w_3)}{(ℌ(z)-w_3)(w_1-w_2)}=\frac{(z-z_2)(z_1-z_3)}{(z-z_3)(z_1-z_2)}.$

La lasta ekvacio povas esti konvertita enen

$\frac{ℌ(z)-w_2}{ℌ(z)-w_3}=\frac{(z-z_2)(w_1-w_2)(z_1-z_3)}{(z-z_3)(w_1-w_3)(z_1-z_2)}.$

Solvanta ĉi tiu ekvacio por $ℌ(z)$ unu ricevas la _sought_ transformo.

Rilato al la fiksa punkta normala formo

Alpreni (tiu, ke, kiu) la punktoj $z_2,z_3$ estas la du (malsama) fiksaj punktoj de la Konverto de Möbius $ℌ$ kio estas $w_2=z_2,w_3=z_3$. Skribi $z_2={\gamma }_1,z_3={\gamma }_2$. La lasta ekvacio

$\frac{ℌ(z)-w_2}{ℌ(z)-w_3}=\frac{(z-z_2)(w_1-w_2)(z_1-z_3)}{(z-z_3)(w_1-w_3)(z_1-z_2)}$

tiam legas

$\frac{ℌ(z)-{\gamma }_1}{ℌ(z)-{\gamma }_2}=\frac{(w_1-{\gamma }_1)(z_1-{\gamma }_2)}{(w_1-{\gamma }_2)(z_1-{\gamma }_1)}\cdot \frac{z-{\gamma }_1}{z-{\gamma }_2}.$

En la antaŭa sekcio sur normala forma Konverto de Möbius kun du fiksaj punktoj ${\gamma }_1,{\gamma }_2$ estis esprimita uzanta la karakteriza konstanto k de la (konverti, konverto) kiel

$\frac{ℌ(z)-{\gamma }_1}{ℌ(z)-{\gamma }_2}=k\frac{z-{\gamma }_1}{z-{\gamma }_2}.$

(Komparanta, Kontrastiganta) ambaŭ esprimoj unu derivas la egaleco

$k=\frac{(w_1-{\gamma }_1)(z_1-{\gamma }_2)}{(w_1-{\gamma }_2)(z_1-{\gamma }_1)}=\text{cr}(w_1,z_1,{\gamma }_1,{\gamma }_2),$

kie $z_1$ estas malsama de la fiksaj punktoj ${\gamma }_1,{\gamma }_2$ kaj $w_1=ℌ(z_1)$ estas la bildo de z₁ sub $ℌ$. En aparta la kruci-rilato $\text{cr}(ℌ(z),z,{\gamma }_1,{\gamma }_2)$ ne dependi sur la elekto de la punkto z (malsama de la du fiksaj punktoj) kaj estas egala al la karakteriza konstanto.

Vidu ankaŭ

• August Ferdinand Möbius
• Grupo de Fuchs
• Hiperbola geometrio
• Inversa ringa geometrio
• Grupo de Klein
• Lorenca grupo
• Modula grupo
• Poincaré-duonebena modelo
• Projekcia geometrio
• Dulineara konverto

Referencoj

• (Celita je ne-matematikistoj, provizas bonegan montraĵon pri teorio kaj rezultoj, riĉe ilustrita per figuroj.)

• (Vidi ĉapitrojn 3-5 de ĉi tiu klasika libro por bela enkonduko al la Rimana sfero, stereografia projekcio, kaj Möbius-transformoj.)

• (Vidu ĉapitron 3 por bele ilustrita enkonduko al transformoj de Möbius inkludanta ilian klasifikon)

• Vidi ĉapitron 2.

• (Vidi Ĉapitron 2 por diversaj izomorfioj, kaj por la Lorenca grupo vidita kiel Galezagrupo.)

• (Vidi ĉapitron 6 por la klasifiko, supren al konjugacio de la kruca algebro de la Lorenca grupo.)

Eksteraj ligiloj

• A java-apleto permesanta precizigi transformon tra ĝiaj fiksaj punktoj kaj tiel plu povas troviĝi je uzantas)._bigpond_._com_/_pmurray_/Javo/_MoebApplet_.html.