Teoremo de Taleso
En matematiko ekzistas du teoremoj nomitaj la teoremo de Taleso, laŭ Taleso el Mileto.
La unua teoremo
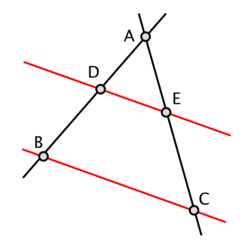
En eŭklida geometrio, la teoremo de Taleso asertas, ke, se paralelaj linioj traversas du flankojn de angulo, tiam la segmentoj (de la du flankoj) rilatas en la sama proporcio. Ekzemple, en la ĉi-kuna desegno, se , Tiam
Laŭ rilatumo eblas atingi aldonajn egalaĵojn, kiel
Etendoj
Unua etendo
La unua etendo asertas, ke la proporcio de la sekcioj, kiujn la angulo intersekcas de la paralelaj linioj, estas ankaŭ egala al la proporcio inter la partoj, kiujn la paralelaj linioj sekcas de la angulaj merkatoj. Ekzemple, en la maldekstra desegno, se , Tiam
Dua etendo

La simpla teoremo de Taleso rilatas nur al kazo, kie la paralelaj linioj estas de la sama flanko de la vertico de la angulo. La dua etendo diras, ke la teoremo de Taleso estas vera eĉ se la linioj ne estas de la sama flanko de la vertico de la angulo. Ekzemple, en la maldekstra desegno, se , Tiam
Pruvo
La teoremo mem
konstruu kaj kaj .
Ekzamenu la triangulon Kaj la triangulo .
En ĉi tiuj du trianguloj, estas komuna latero, kaj perpendikularo de al egalas al perpendikularo de al. (Ĉar )
Tial, la areoj de ĉi tiuj trianguloj estas egalaj, t.e.
Se vi aldonas al la du flankoj de la egalo la areon de la triangulo, Akceptu
Mallevu perpendikularon de al , Kaj perpendikularon de al .
Ĉar triangula areo egalas al duono de la produkto de flanko ĉe ĝia perpendikularo, ni ricevas:
Reordigo kondukos nin al la sekva rezulto:
Nun rigardu la triangulojn kaj-
La areoj de ĉi tiuj trianguloj ankaŭ egalas, ĉar ili havas komunan bazon kaj ilia perpendikularo estas la distanco inter la paraleloj
Ni uzos la perpendikularojn, kiujn ni mallevis, por esprimi la areojn de la trianguloj kaj- :
Reordigo kondukos al la sekva rezulto:
Ni komparos la rilaton kaj ricevos:
Post interŝanĝado de lokoj sur la diagonalo, vi ricevas:
Unua etendo
Konstruu kaj .
Ekzamenu la triangulon Kaj la triangulo .
En ĉi tiuj du trianguloj, latero, kaj perpendikularo de al- egala al perpendikularo de Al- . (Ĉar )
Tial, la areoj de ĉi tiuj trianguloj estas egalaj, t.e.
Se vi aldonas al la du flankoj la areon de la triangulo , Akceptu
Dividu la du flankojn en la triangulan areon , Kaj ni ricevos
Mallevu perpendikularo de- al- , Kaj perpendikularo de- Al- .
Ĉar triangula areo egalas al duono de la produkto de flanko ĉe ĝia alteco, vi ricevas:
Post redukto, vi ricevas:
Dua etendo
Pri la sekcio , Marku punkton , tiel ke- . Ekde- Kaj- Paralelogramo do
Sekve, laŭ la teoremo de Taleso, (kiam temas pri angulo )
Ni metu , Kaj ni ricevos
La dua teoremo

En eŭklida geometrio, la teoremo de Taleso asertas, ke la angulo metita sur diametro en cirklo estas orto : se la punktoj , kaj- estas metitaj sur cirklon kaj la linion trapasas la centron de la cirklo, tiam la angulon estas orta.
Ĉi tiu teoremo probable estis jam empirie konata de Egiptanoj kaj babilonanoj, sed ili ne traktis geometriajn pruvojn, kaj ĉiukaze ankaŭ ne donis pruvon por ĉi tiu teoremo. La unua pruvo estas atribuita al la greka filozofo kaj geometristo Taleso el Mileto, laŭ kiu la leĝo estas nomita.
Pruvo
La pruvo baziĝas sur du konataj faktoj, kiujn Eŭklido ankaŭ atribuas al Taleso en sia libro Elementoj.
- La bazaj anguloj en Izocela triangulo egalas unu al la alia.
- La sumo de la anguloj en triangulo egalas al 180 gradoj.

Markita per La centro de la cirklo. Ĉar la punktoj , kaj- Metitaj sur la cirklon, okazas , Sekve la trianguloj kaj- Ambaŭ estas izocelaj. Laŭ la unua supre menciita fakto, ankaŭ . Ni markos la unuan angulon per litero , Kaj la dua per . La sumo de la anguloj en la triangulo ABC estas , duonigu la du flankojn kaj ricevos .
Simetria vortigo kaj ĝeneraligo
La teoremo, kiel ĉi tie prezentita, asertas, ke se triangulo estas blokita en cirklo tiel, ke unu el ĝiaj flankoj estas la diametro de la cirklo, tiam la triangulo estas ortangula. La malo ankaŭ validas, kaj jen kiel la frazo povas esti vortumita simetrie :
- La centro de cirklo, kiu blokas triangulon, ripozas sur unu el la lateroj, se kaj nur se la triangulo estas ortangula.
La Teoremo de Taleso estas aparta kazo de la teoremo per kiu centra angulo projektita sur hordo en cirklo estas ĉiam duobla de la samprojektita angulo ĉe la cirkonferenco.
Origino de la nomo
La nomo por ambaŭ teoremoj ricevis en la dua duono de la 19-a jarcento en Francio kaj Italio unuflanke kaj en Germanio aliflanke. Samtempe intereso pri la historio de matematiko kaj spurado de ĝiaj originoj pliiĝis. Ligita al tio estis didaktika bezono: doni nomojn al teoremoj, kiuj estis konsiderataj centraj por lernolibroj. La elekto de nomoj de matematikistoj el la pratempo kaj precipe el antikva Grekio, la lulilo de okcidenta kulturo, eble transdonus gravajn kaj tradiciajn valorojn. Ĉi tiuj du teoremoj (aŭ tre proksimaj al ili) estas inter la kvin teoremoj konataj kiel la atingoj de Taleso, sed ne ekzistas indico, ke li pruvis ilin.
La elekto de malsamaj teoremoj en Francio kaj Germanio estas lingva evidenteco en ambaŭ landoj pri la aliro al geometrio. La francoj estis influitaj de la libro de Adrien-Marie Legendre "Fundamentoj en Geometrio". Legendre antaŭis la studon de la cirklo (Ĉapitro 3 en la Elementoj de Eŭklida) al la studo de la triangulo kaj la paralelogramo (Ĉapitroj 1 kaj 2). La affinea geometrio kaj projekcia geometrio, kiuj disvolviĝis tiutempe, metis la rilaton inter intervaloj en la centron, dum en Eŭklido ili aperas en la ĉapitro ses kiel triangulaj similecoj. La inversigo de la ordo de la ĉapitroj indikis grandan ŝanĝon en percepto. La francoj do elektis leĝon, kiu diskutis la rilaton inter intervaloj. La germanoj rekomendis eŭklidan geometrion, aliĝis al la ordo en tiu libro kaj al la centreco de la teoremo de Pitagoro kaj tial elektis teoremon, kiu ligas al la temo de la triangulo (triangulo ĉirkaŭita en cirklo).
Landoj trafitaj de la franca aliro estis: Hispanio, Belgio kaj Rusujo. Landoj trafitaj de la germana aliro estis: Aŭstrio, Hungario kaj Czechoslovakio. Ĝis la dudekaj jaroj de la 20-a jarcento lernolibroj en Grekio elektis la germanan aliron, sed tiam ĝi estis anstataŭigita per la franca aliro. En Anglujo kaj Usono, la nomo de Taleso tiam ne estis uzata por ĉi tiuj provoj.